Janjang geometri

Dalam bidang matematik, janjang geometri ialah sejenis janjang dengan nisbah yang malar antara sebutan-sebutannya. Sebagai contoh,

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots$

ialah janjang geometri kerana setiap sebutan (kecuali sebutan pertama) diperolehi dengan mendarab sebutan sebelumnya dengan $\frac{1}{2}$.

Hasil tambah

Rumus untuk hasil tambah janjang geometri ialah

$a+ar+a{r}^2+a{r}^3+\cdots +a{r}^n=\sum _{k=0}^{n}a{r}^k=a\frac{1-r^{n+1}}{1-r},$

di mana $a$ ialah sebutan pertama dan $r$ ialah nisbah sepunya, dan $r\ne 1$. Rumus ini diperoleh dengan langkah-langkah berikut:

$\begin{array}{cc}& \text{Katakan }s=1+r+r^2+r^3+\cdots +r^n.\\ & \text{Maka }rs=r+r^2+r^3+r^4+\cdots +r^n+r^{n+1}.\\ & \text{Maka }s-rs=s(1-r)=1-r^{n+1},\text{ jadi }s=\frac{1-r^{n+1}}{1-r}.\end{array}$

Rumus tadi boleh dihasilkan dengan mendarab dengan $a$.

Bila $n$ mendekati ketakterhinggaan, nilai mutlak bagi $r$ mestilah lebih kecil daripada 1 supaya janjang tersebut menumpu. Hasil tambah tadi kemudiannya menjadi

$s=\sum _{k=0}^{\mathrm{\infty }}a{r}^k=\frac{a}{1-r}=a+ar+a{r}^2+a{r}^3+a{r}^4+\cdots .$

Bila $a=1$, permudahkan lagi:

$1+r+r^2+r^3+\cdots =\frac{1}{1-r},$

dengan ungkapan sebelah kiri adalah janjang geometri dengan nisbah sepunya $r$. Kita memperoleh rumus ini:

$\begin{array}{cc}& \text{Katakan }s=1+r+r^2+r^3+\cdots .\\ & \text{Maka }rs=r+r^2+r^3+\cdots .\\ & \text{Maka }s-rs=1,\text{ jadi }s(1-r)=1,\text{ jadi }s=\frac{1}{1-r}.\end{array}$

Rumus am ini sah jika didarab dengan $a$.

Rumus ini hanya sah untuk siri yang menumpu (iaitu bila nilai mutlak $r$ kebih kecil daripada 1). Sebagai contoh, hasil tambah ini tak tertakrif bila $r=10$ meskipun rumus itu menghasilkan $s=-\frac{1}{9}$.

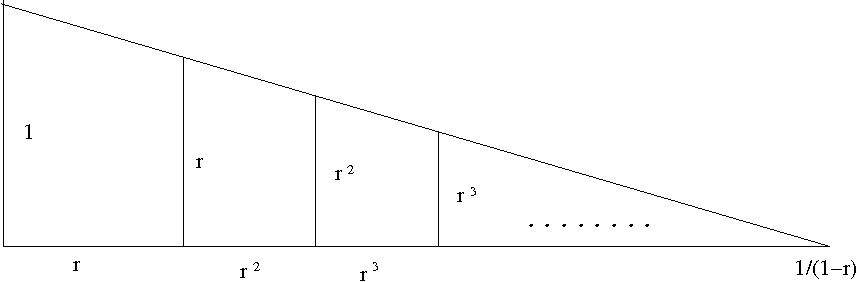
Berikut ialah gambaran bagi janjang geometri oleh E.Hairer dan G.Wanner, Analysis by Its History, bab III.2, rajah 2.1, m/s 188, Springer 1996: